5 Network analysis

5 Network analysis#

import networkx as nx
import pandas as pd
import matplotlib.pyplot as plt

5.1 Basic concepts of network#

  • A network is frequently used interchangeably with a graph, but it typically highlights real-world applications and is commonly associated with social relationships (social networks), and built environments (road networks).

  • A graph (\(G\)) is a mathematical structure used to model pairwise relations between objects. It consists of a set of vertices (nodes) and a set of edges (links) that connect pairs of vertices.

Graph Type

Graph Type

Description

NetworkX Class

Undirected Graph

A graph where edges have no direction.

Graph

Directed Graph

A graph where edges have a direction, indicated by an arrow.

DiGraph

Multi-(undirected) Graph

An undirected graph with parallel edges.

MultiGraph

Multi-directed Graph

A directed graph with parallel edges.

MultiDiGraph

Note: All types of graphs can have self-loops.

5.2 Measurements for nodes and edges#

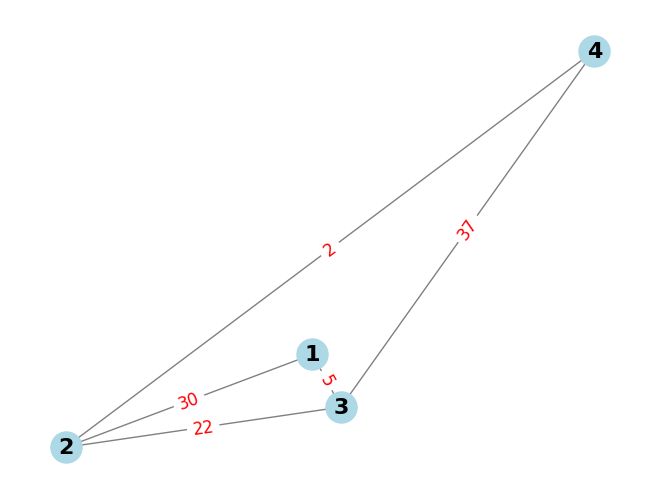
# Create an empty undirected graph
G = nx.Graph()

# Add edge with weight
G.add_edge(1, 2, weight=30)
G.add_edge(1, 3, weight=5)
G.add_edge(2, 3, weight=22)
G.add_edge(2, 4, weight=2)
G.add_edge(3, 4, weight=37)

# Print edge infos
print(G.edges(data=True))

[(1, 2, {'weight': 30}), (1, 3, {'weight': 5}), (2, 3, {'weight': 22}), (2, 4, {'weight': 2}), (3, 4, {'weight': 37})]

# Print node infos, the {} represents the node attributes for each node, e.g, you can input {'attribute_name': 'value'}
print(G.nodes(data=True))

[(1, {}), (2, {}), (3, {}), (4, {})]

# Print weight info
weights = nx.get_edge_attributes(G, 'weight')
weights

{(1, 2): 30, (1, 3): 5, (2, 3): 22, (2, 4): 2, (3, 4): 37}

# Network draw 
pos = nx.random_layout(G)

nx.draw(G, pos, with_labels=True, node_color='lightblue', edge_color='gray', node_size=500, font_size=16, font_weight='bold')

# Draw edge labels (weights)
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_color='red', font_size=12)

{(1, 2): Text(0.5561991977914811, 0.12568247125450527, '30'),
 (1, 3): Text(0.7006559471724646, 0.1625788871207906, '5'),
 (2, 3): Text(0.5711164605781995, 0.0773496395248637, '22'),
 (2, 4): Text(0.7041137349515878, 0.4039085552972916, '2'),
 (3, 4): Text(0.8485686428703795, 0.4408032318889426, '37')}
_images/d133133cf86158db0af426f00394f24945326faa661c9ad4384ef2339c85cb72.png

5.2.1 Degree centrality of nodes#

The degree centrality values are normalized by dividing by the maximum possible degree in a simple graph n-1 where n is the number of nodes in \(G\).

# networkx
nx.degree_centrality(G)

{1: 0.6666666666666666, 2: 1.0, 3: 1.0, 4: 0.6666666666666666}

5.2.2 Closeness centrality of nodes#

  • Closeness centrality of a node \(u\) is the reciprocal of the average shortest path distance to \(u\) over all \(n-1\) reachable nodes.

  • \(G =(U,V)\).

\(C(v) = \frac{n-1}{\sum_{v =1}^{n-1} d(v, u)}\)

  • where \(d(v, u)\) is the shortest-path distance between v and u, and n-1 is the number of nodes reachable from \(u\).

Shortest path and distance

  • 1->2 : 1,3,2 (5+22 = 27)

  • 1->3: 1,3 (5)

  • 1->4: 1,3,2,4 (5+22+2=29)

  • 2->3: 2,3 (22)

  • 2->4: 2,4 (2)

  • 3->4: 3,2,4 (22+2=24)

# use networkx to get shoreat path distance 
nx.shortest_path_length(G, 1, 2, weight='weight')

27

nx.shortest_path_length(G, 1, 3, weight='weight')

5

nx.shortest_path_length(G, 1, 4, weight='weight')

29

nx.shortest_path_length(G, 2, 3, weight='weight')

22

nx.shortest_path_length(G, 2, 4, weight='weight')

2

nx.shortest_path_length(G, 3, 4, weight='weight')

24

# cc of node 1
(4-1) / (27 + 5 + 29)

0.04918032786885246

# cc of node 2
(4-1) / (27 + 22 + 2)

0.058823529411764705

# cc of node3
(4-1) / (5 + 22 + 24)

0.058823529411764705

# cc of node 4
(4-1) / (29 + 2 + 24)

0.05454545454545454

# use nx to get cc
nx.closeness_centrality(G, distance='weight')

{1: 0.04918032786885246,
 2: 0.058823529411764705,
 3: 0.058823529411764705,
 4: 0.05454545454545454}

5.2.3 Betweenness centrality of nodes#

Betweenness centrality of a node \(v\) is the sum of the fraction of all-pairs shortest paths that pass through \(v\).

\(C_B(v) = \sum_{s,t \in V} \frac{\sigma({s,t |v })}{\sigma({s, t})}\)

  • where \(V\) is the set of nodes,

  • \(\sigma({s, t})\) is the number of shortest paths,

  • \(\sigma({s,t |v })\) is the number of those paths passing through some node \(v\) other than \(s,t\).

\(\text{Normalization } C_B \text{ of node} = \frac{ C_B \text{ of nodes} }{ \text{Normalization Factor} }\)

\(\text{Normalization Factor (NF) for undirected graph} = \frac{(n-1) \cdot (n-2)}{2}\)

\(n\) is the nodes numbers.

# NF
(4-1)*(4-2)/2

3.0

# Normalized betweenness centrality of node 1
0/3

0.0

# Normalized betweenness centrality of node 2
2/3

0.6666666666666666

# Normalized betweenness centrality of node 3
2/3

0.6666666666666666

# Normalized betweenness centrality of node 4
0/4

0.0

# get betweenness centrality using nx
nx.betweenness_centrality(G,  weight='weight', normalized=True)

{1: 0.0, 2: 0.6666666666666666, 3: 0.6666666666666666, 4: 0.0}

5.2.4 Betweenness centrality of edges#

Betweenness centrality of an edge \(e\) is the sum of the fraction of all-pairs shortest paths that pass through \(e\).

\(C_B(e) = \sum_{s,t \in V} \frac{\sigma({s,t |e})}{\sigma({s, t})}\)

  • where \(V\) is the set of nodes,

  • \(\sigma({s, t})\) is the number of shortest paths (\({s, t}\)),

  • \(\sigma({s,t |e })\) is the number of those paths passing through edge \(e\).

\(\text{Normalization } C_B \text{ of edges} = \frac{ C_B \text{ of edges} }{ \text{Normalization Factor} }\)

\(\text{Normalization Factor (NF) for undirected graph} = \frac{n(n-1)}{2}\)

n is the nodes numbers.

# Normalized betweenness centrality of edge (1,2)
0/6

0.0

# Normalized betweenness centrality of edge (1,3)
3/6

0.5

# Normalized betweenness centrality of edge (2,3)
4/6

0.6666666666666666

# Normalized betweenness centrality of edge (2,4)
3/6

0.5

# Normalized betweenness centrality of edge (3,4)
0/6

0.0

# get edge_betweenness_centrality using nx
nx.edge_betweenness_centrality(G,  weight='weight', normalized=True)

{(1, 2): 0.0,
 (1, 3): 0.5,
 (2, 3): 0.6666666666666666,
 (2, 4): 0.5,
 (3, 4): 0.0}

Note: If we create a DiGraph, are measurements still the same?

Gd = nx.DiGraph()

Gd.add_edge(1, 2, weight=30)

Gd.add_edge(1, 3, weight=5)

Gd.add_edge(2, 3, weight=22)

Gd.add_edge(2, 4, weight=2)

Gd.add_edge(3, 4, weight=37)

Contents